Combinational circuits part 2

Truth table of 3 line to 8 line decoder:


 4.BCD to seven segment decoder:
It consists of a seven segment display consisting of seven light emitting diodes.The segments are denoted by letters a-g .By illuminating various combinations of segments numbers from 0-9 can be depicted.
In electronics there are two important types of 7-segment LED digital display.

• 1. The Common Cathode Display (CCD) – In the common cathode display, all the cathode connections of the LED’s are joined together to logic “0” or ground. The individual segments are illuminated by application of a “HIGH”, logic “1” signal to the individual Anode terminals.
• 2. The Common Anode Display (CAD) – In the common anode display, all the anode connections of the LED’s are joined together to logic “1” and the individual segments are illuminated by connecting the individual Cathode terminals to a “LOW”, logic “0” signal.

5.Encoder:
1.BCD adder:
The steps followed in a BCD adder can be considered after considering the steps of BCD addition:
1.firstly the two BCD code groups are added for each decimal digit position using ordinary binary addition.
2.For those positions where the sum is 9 or less,the sum is in proper BCD format and no correction is needed.
3.When the sum of 2 digits is greater than 9 a correction of 0110 should be added to the sum,to produce proper BCD result.this will produce a carry to be added to the next decimal position.

In accordance with above rules the BCD adder performs following actions :
1.BCD adder adds the two numbers inputed and generates the output.If the sum is less than 9 then the output corresponds to the result.
2.If the sum is greater than 9(1001) then 0110 is added to the result and carry bit generated is taken to the next decimal position.





Above diagram showed us the realisation of BCD adder using two 4-bit adders and a correction detector circuit.
Only when the output carry is equal to 1 does the number 0110 be added to the binary sum to generate the new sum and carry.

2.Comparator:

A comparator is a logic circuit used to compare two binary numbers.
the X-nor gate is a basic comprator because its output is a 1 only if its two input bits are equal.

A comparator signifying which of the two numbers is greater is more complex.
if A=A3A2A1A0 and B=B3B2B1B0 be two four bit numbers then the steps followed by the comparator are:
1.Compare the most significant bits A3 and B3 of the two numbers.If A3 is a 1 and B3 is a 0 then A>B
if and only if A and B coincide go to step 2.
2.Compare the bits A2 and B2 of the numbers.if A2=1 and B2=0,A>B; if A2=0 and B2=1,A<B.if both the values coincide then goto step 3.
3.Compare the bits A1 and B1 of the numbers.If A1=1 and B1=0,A>B ;if A1=0 and B1=1,A<B if both the values coincide then goto step 4.
4..Compare the bits A0 and B0 of the numbers.If A0=1 and B0=0,A>B;if A0=0 and B0=1,A<B,if both the values coincide then A=B.


 

 

Above map shows steps for configuring a 2-bit comparator.


3.Decoder:
A decoder is a logic circuit that converts an N bit binary input code into M output lines such that only one output line is activated for each combination of inputs.
 a 3line to 8-line decoder has 3 inputs and 8 outputs as the name suggests.For active high outputs AND gates are used and for active low outputs NAND gates are used.

Logic diagram of 3line to 8 line decoder:
 

An encoder has a number of input lines only one of which is activated at a given time and produces an N-bit output code depending on which input is activated.
In short it performs the reverse of the operation performed by a decoder.







Octal to binary encoder

 
truth table is given below:





 6.Multiplexer
This logic circuit selects 1 out of several inputs and gives it as the output.

7.Demultiplexer:

A demultiplexer has a single input line and several output lines.Depending on the select signals the output is generated.

Digital circuits : Combinational circuits

Various logical operations can be performed by interconnection of the appropriate logic elements.

We will be seeing the most commonly used combinational circuits in this chapter.

1.HALF ADDER:

An adder is a combinational circuit which adds two input numbers to give a sum and a carry element.

Adders are used to add either binary numbers ,x-s 3 code etc.

A half adder is a combinational arithmetic circuit which adds two numbers and give a sum bit and a carry bit.

If  A and B are the input bits, then sum bit (S) is the X-OR of A and B  and the carry bit (C) will be the AND of A and B. From this it is clear that a half adder circuit can be easily constructed using one X-OR gate and one AND gate.
 

2. Full adder:

A full adder is an arithmetic circuit that adds two bits and a carry and outputs a sum bit and a carry bit.

Even though a full adder can be constructed using only two half adders,the disadvantage is that the bits must pass through several gates in succession which makes the propagation delay greater than the configuration using AOI logic implementation.Below given is the implementation of full adder using AOI logic.

 

3.Half subtractor:

A subtractor is an arithmetic circuit used for subtracting the LSB of the subtrahend from the LSB of the minuend.When subtraction is performed the output is a difference bit and a borrow bit.

 

For consideration of borrow element from a previous subtraction the full subtractor circuit mentioned below is used.

4.Full subtractor:

The full subtractor is a combinational circuit which is used to perform subtraction of three input bits: the minuend , subtrahend 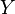, and borrow in 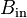. The full subtractor generates two output bits: the difference 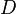and borrow out .

                                                                 

Full subtractor logic diagram:

The full subtractor circuit can also be realised using  universal gates that is using only nand and nor gates.

5.Look ahead carry adder:

A carry-lookahead adder (CLA) or fast adder is a type of adder used in digital logic. A carry-lookahead adder improves speed by reducing the amount of time required to determine carry bits. It can be contrasted with the simpler, but usually slower, ripple carry adder for which the carry bit is calculated alongside the sum bit, and each bit must wait until the previous carry has been calculated to begin calculating its own result and carry bits (see adder for detail on ripple carry adders). The carry-lookahead adder calculates one or more carry bits before the sum, which reduces the wait time to calculate the result of the larger value bits. 

To reduce the computation time, there are faster ways to add two binary numbers by using carry lookahead adders. They work by creating two signals P and G known to be Carry Propagator and Carry Generator. The carry propagator is propagated to the next level whereas the carry generator is used to generate the output carry ,regardless of input carry. The block diagram of a 4-bit Carry Lookahead Adder is shown here below -

The corresponding boolean expressions are given here to construct a carry lookahead adder. In the carry-lookahead circuit we ned to generate the two signals carry propagator(P) and carry generator(G),

P_i = A_i ⊕ B_i

G_i = A_i · B_i

The output sum and carry can be expressed as

Sum_i = P_i ⊕ C_i

C_i+1 = G_i + ( P_i · C_i)

Having these we could design the circuit. We can now write the Boolean function for the carry output of each stage and substitute for each Ci its value from the previous equations:

C₁ = G₀ + P₀ · C₀

C₂ = G₁ + P₁ · C₁ = G₁ + P₁ · G₀ + P₁ · P₀ · C₀

C₃ = G₂ + P₂ · C₂ = G₂ P₂ · G₁ + P₂ · P₁ · G₀ + P₂ · P₁ · P₀ · C₀

C₄ = G₃ + P₃ · C₃ = G₃ P₃ · G₂ P₃ · P₂ · G₁ + P₃ · P₂ · P₁ · G₀ + P₃ · P₂ · P₁ · P₀ · C₀

 

Digital circuits:logic gates

Logic gates are the basic building blocks of any electronic network.They have two or more inputs and only one output.The relationship between the output and input is based on a certain logic.
Mentioned below are the symbols of the logic gates.

The AND,OR and NOT gates are the gates we commonly come across in  our circuits.
Apart from these NAND and NOR gates can also be to configure an electronic circuit.Only NAND gates or only NOR gates can be used to prepare a logic circuit.Hence the NAND or NOR gates are called as universal gates.
1.AND gate

The AND gate gives a high output only when all its inputs are high.

2.OR gate
The or gate gives a low output when all its inputs are low.

3.NOT gate:

The not gate perform the complement of the input signal.

4. NAND gate:
The complement of the AND gate is achieved by a NAND gate.



The NAND gate gives a low output only when all its inputs are high.







Since the output assumes the high state even if one of its inputs is low NAND gate is also called as active low OR gate.

5.NOR gate
The complement of the OR gate gives the NOR gate.
The expression for a NOR gate is the result of adding a NOT gate to the OR gate.




Since its output assumes the high state only when all its inputs are zero, a nor gate is also called active low AND gate.

6.EX-OR gate:
The output is in logic one if any one of the inputs is 1.Since the output is 1 when the inputs are unequal the exclusive or gate is called inequality detector.


The output expression for inputs A and B can be represented as Y =A'B+AB'

7.EX-NOR gate:
An X-NOR gate is the complement of EX-OR gate.The output of X-NOR gate is low when even if only one of the inputs is high.The output takes a logic 1 when both of the inputs are 1 or 0.







Since the output is 1 only when both inputs are same the EX-NOR gate is also called as equality detector.